卷积公式推导过程(常用卷积公式表大全)

卷积公式推导过程

这里的[H,W,C]是一个3维数组,区别于我们常见的一维数组(也叫向量)和二维数组(也叫矩阵),3维或更高维的数组,我们称之为张量(英文名为Tensor)。

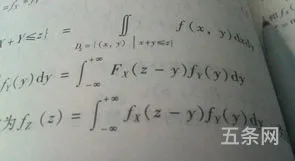
整个*网络的运行就像是Tensor在一层一层的算法之间流动一样,因此有个大名鼎鼎的框架叫做TensorFlow,意为Tensor的流动。

有了这些基本概念后,就可以说,一个卷积运算就是一个卷积算子,也就是一个OP。那么输入的图片是输入Tensor(inputtensor),卷积核就是这个卷积算

这三个维度分别用3个字母代替,分别是H(Height,对应的是长这一维度),W(Width,对应的是宽这一维度),C(Channel,对应的是通道这一维度)。

Tensor这个概念很重要,在几乎所有的*网络推理、训练框架里面,*网络算法的输入和输出数据都会被叫作Tensor。

常用卷积公式表大全

对于一张长宽为224x224的RGB图像,我们可以用以下的方法来表示这种图片的“数据形状”,[H,W,C]=[224,224,3]。

再将上述结论一般化一下,上述这个结论都是基于每次“挨巴掌”都是鼓起同样高度的包,但是如果我们假设,白天*状态好,挨一巴掌鼓起来的包小一些,晚上反之会高一些,那么一天之中不同时刻t,“挨巴掌”后的鼓包高度定义为

比如当我们设计一个通带为[0,f]的低通滤波器时,可以将此低通滤波器频域表达式经过傅里叶拟变换,可以得到滤波器的时域表达式,使用此时域表达式与目标信号计算卷积,就可以实现低通滤波了。

比如上述例子里:g(0)=1,因为挨巴掌的一瞬间鼓包高度变成了1;而当n≥1时,g(n)则变为0。注意上述g(n)规则是我们在这个例子里定义的,不同的场合会不尽相同。

看一下下图,红线的方波代表“打了一巴掌”,蓝线是肿起来的鼓包的高度。假设鼓包一天的时间(24小时)可以完全回复,也就是高度会变为0。

概率论卷积公式怎么用

如果进一步增加扇巴掌的频次,如果时间间隔小于24小时,那么第二次的鼓包就会叠加上上一次没有消除的鼓包高度,对应鼓包高度会像下图这样:

在此前提下,h1的值就等于g(0),h2的值等于g(0.1),h3的值等于g(0.2),h4的值等于g(0.3),这不难理解吧。

因为傅里叶变换本身就是将一个函数表示为正交函数的线性组合,因此我们将拉普拉斯矩阵的特征向量矩阵作为傅里叶变换的基

SCNN将卷积从图像推广到图结构,是GNN中非常经典的一个模型,但仍然具有一些问题,例如没有继承“感受野”的性质,以及计算复杂度是

自己在入门图*网络时,学习到谱域图卷积的时候,虽然有很多不错的教程,无奈看地比较困难。主要还是因为诸如傅里叶卷积和一堆矩阵看起来十分抽象,无法将其和图的各种维度联系起来。