资本资产定价模型公式(资产定价模型的六个基本假设)

资本资产定价模型公式

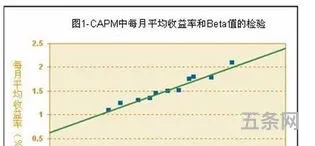
资本资产定价模型(CapitalAssetPricingModel,CAPM)是描述资本市场定价的经济模型,用于估计资产期望收益率的理论框架。CAPM的基本公式如下:

尽管CAPM在实际应用中存在一些争议和局限性,但它仍然是金融学和投资领域中的基础工具之一,为理解风险和收益的关系提供了重要的框架。

资本资产定价理论(CapitalAssetPricingModel)实际上是上述投资组合理论的延伸。在Markowitz投资组合理论的基础上,假设市场上存在利率为

Markowitz投资组合理论的基本假设是投资者会尽可能的规避风险。如果两个资产拥有相同预期回报,投资者会选择其中风险小的那一个。只有在获得更高预期回报的前提下,投资者才会承担更大风险。

资产定价模型的六个基本假设

总结一下,我们用两个优化问题的求解,从数学上导出了Markowitz投资组合理论和资本市场线CML,最后我们简单的讨论了Beta系数。

大部分讲解CAPM理论的文章都从资本市场线CML和Beta系数讲起,缺少对模型提出和数学推导的说明,有的时候确实很难让人理解(至少我是这样的)。

此时,存在最小方差资产组合(MinimumVariancePortfolioMVP),即用方差量化风险时,风险最小的投资组合,此时

种资产与市场组合构成的这个投资组合也应该有一个投资前沿,因此该点处的斜率等于资产市场线性的斜率,即

资本成本三个公式

本文将从基础假设开始,从数学公式推导Markowitz投资组合理论,得到风险投资前沿。加入无风险资产后,推出资本市场线CML,并进一步用期望收益率-方差风险图解释其中的关系,最终我们会讨论Beta系数。

其中的双曲关系我们称之为“有效投资前沿”,它对应的金融解释是:不存在无风险资产时,某确定总收益期望时,最合理的投资权重分配。而其中的线*,即存在无风险资产时的有效前沿,称为资本市场线(CapitalMarketLine),它对应的金融解释是:存在无风险资产时,某确定总收益期望时,最合理的投资权重分配。

备注:市场组合的风险收益率=(Rm-Rf),(Rm-Rf)常见表述:市场(平均)风险溢酬(溢价、补偿率、附加率)、风险收益率、风险价格,形容的是市场当中风险的收益率,强调的是在无风险收益率基础之上多出来的那部分(全部带风险两字),Rf是无风险收益率,常用国债利率替代。

甲公.司持有A、B两种证券构成的投资组合,假定资本资产定价模型成立。其中A证券的必要收益率为21%,β系数为1.6;B证券的必要收益率为30%,β系数为2.5。公.司拟将C证券加入投资组合以降低投资风险,A、B、C三种证券的投资比重设定为2.5:1:1.5,并使得投资组合的β系数为1.75。