贝叶斯纳什均衡怎么求(精炼贝叶斯均衡四个要求)

贝叶斯纳什均衡怎么求

即参与人i选择行动a的总概率是每一种类型的i选择a的条件概率p(a|q)的加权平均,权数是他属于每种类型的先验概率p(q)。

并且SKp(q)=1;给定i属于q,i选择a的条件概率为p(a|q),并且SHp(a|q)=1。那么,i选择a的边缘概率(全概率)是

也就是说,i属于q并选择a的联合概率,等于i属于q的先验概率乘以q类型的参与人选择a的概率,或等于i选择a的总概率乘以给定a情况下i属于q的后验概率。

假定有n个参与人,参与人i的类型是qiÎQi,qi是私人信息,pi(q-i|qi)是属于类型qi的参与人i认为其他n-1个参与人属于类型q-i=(qi,,qi-1,qi+1,,qn)的先验概率;

精炼贝叶斯均衡四个要求

一个“合理”的均衡要求,给定每一个参与人有关其他参与人类型的后验信念,参与人的战略组合在每一个后续博弈上构成贝叶斯均衡。

运用子博弈精炼均衡概念的逻辑,将从每一个信息集开始的博弈的剩余部分称为一个“后续博弈”(不同于子博弈,因为子博弈必须开始于单结信息集,并且不能切割信息集),

后验概率Prob(q|a)不仅依赖于先验概率p(q),而且依赖于参与人“认为”i是类型q并选择行动a的条件概率p(a|q)。

这个概念是完全信息动态博弈的子博弈精炼纳什均衡与不完全信息静态均衡的贝叶斯(纳什)均衡的结合。具体来说,精炼贝叶斯均衡是所有参与人战略和信念的一种结合。它满足如下条件:第一,在给定每个参与人有关其他参与人类型的信念的条件下,该参与人的战略选择是最优的。第二,每个参与人关于其他参与人所属类型的信念,都是使用贝叶斯法则从所观察到的行为中获得的。

博弈论贝叶斯法则

假定参与人(在所有可能的情况下)根据贝叶斯法则修正先验信念,并且,每个参与人都假定其他参与人选择的是均衡战略。

如果Prob(a)=0,我们允许Prob(q|a)在[0,1]区间取任何值,只要所取的值与均衡战略相容,即均衡仍然成立。

我们用Prob(q|a)代表这个后验概率,即给定a的情况下,i属于类型q的概率。根据条件概率或乘积概率公式,

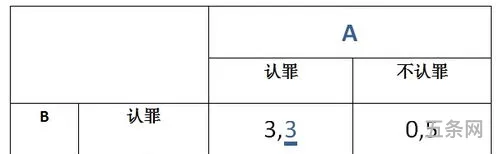
在一个博弈过程中,无论对方的策略选择如何,当事人一方都会选择某个确定的策略,则该策略被称作支配性策略。如果任意一位参与者在其他所有参与者的策略确定的情况下 , 其选择的策略是最优的 , 那么这个组合就被定义为纳什平衡。