初2数学全等(初二全等三角形证明题)

初2数学全等

初二的重要性是不言而喻的,到了初二开设物理科目,地理、生物也要进行毕业会考,这就使孩子学业上的负担大大增加了。不想落后他人,预习复习工作都不能落下。今天,王老师和大家分享的是期末复习|初二数学上册【全等三角形5大判定】必考内容,提分必记!

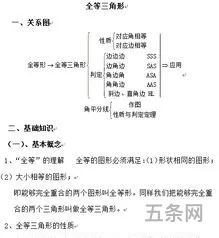
(1)三角形的稳定*:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个*质叫做三角形的稳定*.

通过上面对全等三角形知识点的讲解学习,相信同学们对全等三角形的知识已经能很好的掌握了吧,后面我们进行更多知识点的巩固学习。

注意:因式分解一定要分解到每一个因式都不能再分解为止,否则就是不完全的因式分解,若题目没有明确指出在哪个范围内因式分解,应该是指在有理数范围内因式分解,因此分解因式的结果,必须是几个整式的积的形式。

初二全等三角形证明题

建立了平面直角坐标系后,对于坐标系平面内的任何一点,我们可以确定它的坐标。反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点。

通常采用分组分解法,最后运用十字相乘法分解因式。因此,可以概括为:“一提”、“二套”、“三分组”、“四十字”。

大家都知道,能够完全重合的两个三角形叫做全等三角形(congruenttriangles)。那么接下来的全等三角形知识请同学认真记忆了。

在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。通常,两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。水平的数轴叫做x轴或横轴,铅直的数轴叫做y轴或纵轴,x轴或y轴统称为坐标轴,它们的公共原点o称为直角坐标系的原点。

八年级全等三角形题型总结

对于平面内任意一点c,过点c分别向X轴、Y轴作垂线,垂足在X轴、Y轴上的对应点a,b分别叫做点c的横坐标、纵坐标,有序实数对(a,b)叫做点c的坐标。

公因式确定方法:1系数是整数时取各项最大公约数。2相同字母取最低次幂3系数最大公约数与相同字母取最低次幂的积就是这个多项式各项的公因式。

通过上面对平面直角坐标系的构成知识的讲解学习,希望同学们对上面的内容都能很好的掌握,同学们认真学习吧。

;证明:∵AE⊥EC,AF⊥BF,;A;A;课堂小结判定两个直角三角形全等有哪些方法?;课堂小结“HL”判定方法应满足什么条件?与之前所学的四种判定方法有什么不同?;课堂小结“HL”判定方法应满足什么条件?与之前所学的四种判定方法有什么