刘维尔定理证明(Liouville定理)

刘维尔定理证明

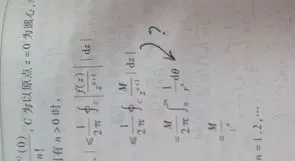
》(Journaldemathématiquespuresetappliquées),并亲自主持了前39卷的编辑出版工作(第1辑,1—20卷,1836—1855年;第2辑,1—19卷,1856—1874年)。该杂志刊登纯粹、

,母亲名叫泰雷兹·巴朗(ThéréseBal-land)。刘维尔是他们的次子,幼时先后就学于科梅西和土尔。1825年他来到

领域所有分支的论文,记录了19世纪中期的40年里数学活动的一部分重要内容,被后人称为《刘维尔杂志》(Liou-ville′sJournal)。

刘维尔不仅与当时一些重要的数学家保持着密切联系并定期发表他们的成果,而且热心地对年轻学者进行指导,为他们发表著作提供机会。最值得一提的当属他编辑发表E.伽罗瓦(Galois)的文章。1832年5月,伽罗瓦在决斗中被杀,刘维尔整理了他的部分遗稿并刊登在1846年的《纯粹与应用数学杂志》上,他在代数方面的独创性工作才得以为世人所知。

Liouville定理

—1838年间,刘维尔曾在成立不久的*高等工艺制造学校讲授数学和力学,但内容均为初级的。为使自己的教学工作保持在大学水平上,他在1836年攻取了博士学位,论文题为“关于函数或其一部分的正弦与

周五上数学课时,无聊地推公式,由于当时正好学了全纯函数的均值性,于是就尝试着把导数形式的柯西积分公式按照均值性质推,然后惊奇地发现,这样做似乎能证明刘维尔定理。

一个闭区间[a,b]嵌套在[A,B]内,是指[a,b]是[A,B]的一个子集。这无异于说满足条件A≤a≤b≤B。我们进一步假定存在一个有界闭区间的序列,其中每个区间嵌套在它前面那个区间内,如像[a1,b1]⊇[a2,b2]⊇[a3,b3]⊇⊇[ak,bk]⊇。这样一个区间序列称为递减序列。利用这种序列我们可以引进实数完备性定义的另外一种形式:

康托尔通过完全不同的方法达到同一目标。他早在1874年发表的论文中就曾许诺“对刘维尔首次证明的定理给出一个新的证明”,无疑他实践了自己的诺言。然而,正如我们所见,在他的论证中没有包含一个特定超越数的例子。这显然是一种非直接的证明。

微分方程刘维尔公式证明

青年时代的康托尔就读于柏林大学,成为魏尔斯特拉斯的门生。在学习期间,他于1867年写了一篇关于数论的专题论文,这是一个完全不同于后来使他闻名于世的领域。他的研究工作把它引向傅里叶级数并且最终转到分析学的基础理论。

风靡美国普林斯顿大学的数学课程读本,教你怎样在数学考试中获得高分,用大量例子和代码全面探讨数学问题提供课程视频和讲义。被誉为“普林斯顿读本”三剑客。

很奇怪,这篇论文的重要意义被它的标题掩盖了,因为关于代数数的结果只不过是文章的真正革命性思想的一个推论,尽管是最有价值的推论。简单地说,这个思想就是一个序列不能穷举一个开区间中的全部实数。正如我们将会看到的那样,康托尔的论证包含了实数的完备性性质,因此把它放在实分析的领域是恰当的。

总之,康托尔证实了在区间(α,β)内存在不出现在原来序列{xk}之中的一点,这就是定理要证明的结果。