混合策略纳什均衡含义(什么叫纯策略纳什均衡)

混合策略纳什均衡含义

通过计算,我们可以得到混合策略纳什均衡为:A投资者选择买入的概率为3/4,选择卖出的概率为1/4;B投资者选择买入的概率为3/4,选择卖出的概率为1/4。

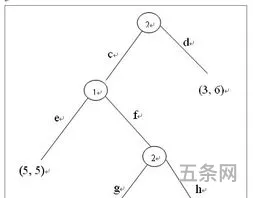
考虑两家公司A和B在某个市场上销售类似的产品,并且可以选择不同的价格策略。下面是两家公司的收益矩阵,数字表示每个公司在不同价格下的收益。

矩阵中的第一个数字表示公司A的收益,第二个数字表示公司B的收益。例如,当公司A选择价格60,公司B选择价格60时,公司A的收益为20,公司B的收益为10。

在这种情况下,公司A的期望收益为10,公司B的期望收益也为10。这个混合策略纳什均衡使得两家公司都无动机改变策略,达到了稳定状态。

假设A投资者以概率p选择买入,以概率(1-p)选择卖出;B投资者以概率q选择买入,以概率(1-q)选择卖出。我们可以计算出每个投资者的期望收益,并找到使得收益最大化的概率p和q。

什么叫纯策略纳什均衡

可知存在两个纯策略纳什均衡(5,5)或(1,1),即:A买入、B买入或者A卖出、B卖出。然而,如果他们采用混合策略,即以一定的概率选择不同的行动方案,可能会得到不同的结果。

通过计算,我们可以得到混合策略纳什均衡为:公司A选择价格60的概率为1/2,选择价格50的概率为1/2;公司B选择价格60的概率为1/2,选择价格50的概率为1/2。

在个人投资中,投资者面临着选择不同投资组合的决策。不同的投资组合可能具有不同的风险和回报特征。通过采用混合策略纳什均衡,投资者可以根据自己的风险偏好和预期回报,以一定的概率选择不同的投资组合。例如,一个投资者可以将资金的50%投资于低风险的固定收益产品,将另外50%投资于高风险的股票市场,以平衡风险和回报。

股票市场是一个典型的博弈环境,投资者在选择买入或卖出时需要考虑其他投资者的行为。假设有两个投资者A和B,可以选择买入或卖出某只股票。他们的收益矩阵如下所示:

混合策略纳什均衡是博弈论中的一个重要概念,能够解释参与者在博弈中的稳定决策状态。通过使用收益矩阵列举实际的例子,我们可以看到混合策略纳什均衡在不同领域的应用,如价格竞争和股票投资。混合策略纳什均衡提供了一种理性决策的方法,使参与者能够在博弈中追求最优的结果。在实际应用中,了解混合策略纳什均衡的概念和计算方法对于分析和预测参与者的行为具有重要意义。

怎么求混合战略纳什均衡

*在资源分配方面面临着复杂的决策问题。例如,考虑一个*需要决定在教育和医疗领域之间分配预算的情况。如果*完全投入教育领域,可能会导致医疗服务的不足,反之亦然。在这种情况下,*可以通过混合策略纳什均衡来平衡资源的分配。*可以以一定的概率将预算分配给教育和医疗领域,以实现最优的资源利用。

可知不存在纯策略纳什均衡。然而,如果两家公司采用混合策略,即以一定的概率选择不同的价格策略,就会得到一个混合策略纳什均衡。

在这种情况下,A投资者的期望收益为13/4,B投资者的期望收益也为13/4。这个混合策略纳什均衡使得两个投资者都无动机改变策略,达到了稳定状态(此时混合策略的纳什均衡收益大于纯策略纳什均衡的(1,1)时的收益,但小于(5,5)时的收益)。

。在纳什均衡中,每个参与者都在其他参与者的策略下作出最佳选择,没有动机再改变自己的策略选择。换句话说,纳什均衡是一个自我稳定的策略组合,没有参与者有动机单方面改变策略。