simulink巴特沃斯滤波器仿真(巴特沃斯滤波器原理)

simulink巴特沃斯滤波器仿真

贝塞尔(Bessel)滤波器具有最平坦的幅度和相位响应。带通（通常为用户关注区域）的相位响应近乎呈线性。Bessel滤波器可用于减少所有IIR滤波器固有的非线性相位失真。

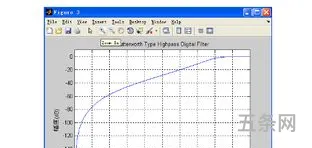
阻带衰减（dB）ChebyshevII型和椭圆形设计的阻带衰减，以dB为单位。可调（Simulink）。

虽然贝塞尔滤波器在它的通频带内提供平坦的幅度和线性相位（即一致的群延时）响应，但它的选择性比同阶（或极数）的巴特沃斯(Butterworth)滤波器或切比雪夫(Chebyshev)滤波器要差。因此，为了达到特定的阻带衰减水平，需要设计更高阶的贝塞尔滤波器，从而它又需要仔细选择放大器和元件来达到最低的噪声和失真度。

阻带边沿频率ChebyshevII型设计的高通和低通频带配置的阻带边沿频率，以rad/s为单位。可调（Simulink）。

巴特沃斯滤波器原理

模拟滤波器设计模块以高通，低通，带通或带阻配置设计和实现Butterworth，I型Chebyshev，II型Chebyshev，椭圆或贝塞尔滤波器。

巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。在振幅的对数对角频率的波特图上，从某一边界角频率开始，振幅随着角频率的增加而逐步减少,趋向负无穷大。

下表列出了每种设计/频段组合的可用参数。对于低通和高通频带配置，这些参数包括通带边沿频率Ωp，阻带边沿频率Ωs，通带纹波Rp和阻带衰减Rs。对于带通和带阻配置，参数包括上下通带边缘频率Ωp1和Ωp2，下限和上阻带边缘频率Ωs1和Ωs2，通带纹波Rp和阻带衰减Rs。频率值以rad/s为单位，纹波和衰减值以dB为单位。

设计方法过滤器设计方法：巴特沃思，I型Chebyshev，II型Chebyshev，椭圆形或Bessel。可调（Simulink）。

带阻滤波器

通带边沿频率Butterworth，ChebyshevI型，椭圆形和贝塞尔设计的高通和低通配置的通带边沿频率（以弧度/秒为单位）。可调（Simulink）。

较低的通带边缘频率Butterworth，ChebyshevI型，椭圆形和贝塞尔设计的带通和带阻配置的较低通带频率，以rad/s为单位。可调（Simulink）。

较低的阻带边沿频率ChebyshevII型设计的带通和带阻配置的较低阻带边沿频率（以rad/s为单位）。可调（Simulink）。

上阻带边沿频率ChebyshevII型设计的带通和带阻滤波器配置的阻带上限频率，以弧度/秒为单位。可调（Simulink）。